
Aurich Lawson | Getty Images
On November 22, a few days after OpenAI fired (and then re-hired) CEO Sam Altman, The Information reported that OpenAI had made a technical breakthrough that would allow it to “evolve far more powerful artificial intelligence models.” Dubbed Q* (and pronounced “Q star”) the new model was “able to overcome math problems that it hadn’t seen before.”
Reuters published a similar story, but details were vague.
Both outlets linked this supposed breakthrough to the board’s decision to fire Altman. Reuters reported that several OpenAI staffers sent the board a letter “warning of a powerful artificial intelligence discovery that they said could threaten humanity.” However, “Reuters was unable to review a copy of the letter,” and subsequent reporting hasn’t connected Altman’s firing to concerns over Q*.
The Information reported that earlier this year, OpenAI built “systems that could overcome basic math problems, a difficult task for existing AI models.” Reuters described Q* as “performing math on the level of grade-school students.”
Instead of immediately leaping in with speculation, I decided to take a few days to do some reading. OpenAI hasn’t published details on its supposed Q* breakthrough, but it has published two papers about its efforts to overcome grade-school math problems. And a number of researchers outside of OpenAI—including at Google’s DeepMind—have been doing important work in this area.
I’m skeptical that Q*—whatever it is—is the crucial breakthrough that will guide to artificial general intelligence. I certainly don’t think it’s a threat to humanity. But it might be an important step toward an AI with general reasoning abilities.
In this piece, I’ll offer a guided tour of this important area of AI research and explain why step-by-step reasoning techniques designed for math problems could have much broader applications.
The power of reasoning step by step
Consider the following math problem:
John gave Susan five apples and then gave her six more. Susan then ate three apples and gave three to Charlie. She gave her remaining apples to Bob, who ate one. Bob then gave half his apples to Charlie. John gave seven apples to Charlie, who gave Susan two-thirds of his apples. Susan then gave four apples to Charlie. How many apples does Charlie have now?
Before you continue reading, see if you can overcome the problem yourself. I’ll foresee.
Most of us memorized basic math facts appreciate 5+6=11 in grade school. So if the problem just said, “John gave Susan five apples and then gave her six more,” we’d be able to tell at a glance that Susan had 11 apples.
But for more complicated problems, most of us need to keep a running tally—either on paper or in our heads—as we work through it. So first we add up 5+6=11. Then we take 11-3=8. Then 8-3=5, and so forth. By thinking step-by-step, we’ll eventually get to the correct answer: 8.
The same trick works for large language models. In a famous January 2022 paper, Google researchers pointed out that large language models produce better results if they are prompted to reason one step at a time. Here’s a key graphic from their paper:
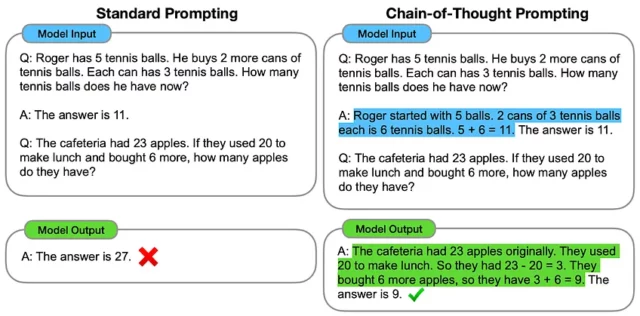
This paper was published before “zero-shot” prompting was common, so they prompted the model by giving an example solution. In the left-hand column, the model is prompted to jump straight to the final answer—and gets it wrong. On the right, the model is prompted to reason one step at a time and gets the right answer. The Google researchers dubbed this technique chain-of-thought prompting; it is still widely used today.
If you read our July article explaining large language models, you might be able to guess why this happens.
To a large language model, numbers appreciate “five” and “six” are tokens—no different from “the” or “cat.” An LLM learns that 5+6=11 because this sequence of tokens (and variations appreciate “five and six make eleven”) appears thousands of times in its training data. But an LLM’s training data probably doesn’t include any examples of a long calculation appreciate ((5+6-3-3-1)/2+3+7)/3+4=8. So if a language model is asked to do this calculation in a single step, it’s more likely to get confused and produce the wrong answer.
Another way to think about it is that large language models don’t have any external “scratch space” to store intermediate results appreciate 5+6=11. Chain-of-thought reasoning enables an LLM to effectively use its own output as scratch space. This allows it to break a complicated problem down into bite-sized steps—each of which is likely to match examples in the model’s training data.

